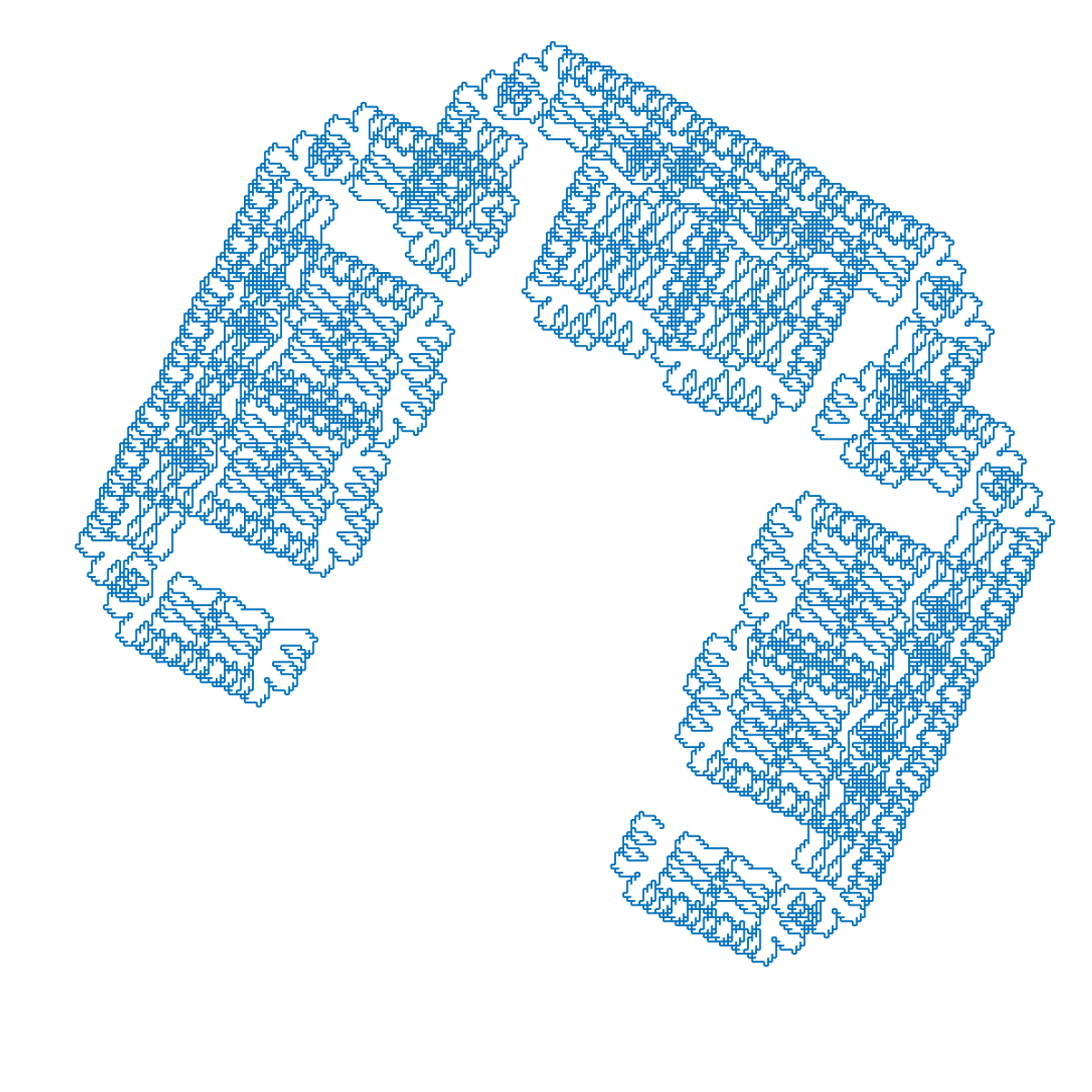Lindenmayer Systems
A string can be converted into a curve using “turtle graphics”.
You can imagine that an ink pen is being dragged along a sheet of paper by a turtle, who will walk forward or change direction depending on the instructions it reads on the string.
The turtle proceeds by reading the string character by character from left to right.
For instance, ‘F’ might mean go forward, and ‘-‘ might mean “turn right”.
Using a string-rewriting system, called a Lindenmayer system or L-system, complicated or even fractal curves can be generated by this method. The code for these images (excluding the plants below) can be found here.
The Dragon Curve
A simple example is the dragon curve. First, we iteratively apply the following rules to the initial string ‘FX’:
- 'X' becomes 'X+YF+'
- 'Y' becomes '-FX-Y'
Then the turtle draws a curve from the resulting string according to the following instructions:
- 'F' means go forward
- '-' means turn left 90 degrees
- '+' means turn right 90 degrees
- 'X' or 'Y' means do nothing
| Dragon Curve (5 iterations) |
Dragon Curve (15 iterations) |
 |
 |
Some Simple Curves
A lot of interesting behaviour occurs even when using only the simpler alphabet {‘F’, ‘-‘, ‘+’} (with the same instructions).
If we consider the starting string ‘F’, there are $3^n$ possible rules of length $n$.
Of course, not all rules are created equal– for instance, the rule ‘F’$\to$’FF’ simply produces a straight line.
Below are some of the more interesting examples.
Shapes
| 'F' $\to$ 'FF++F' (15 iterations) |
'F' $\to$ 'FF++' (15 iterations) |
 |
 |
Tilings
| 'F' $\to$ 'FFF-F' (5 iterations) |
'F' $\to$ 'FFF-F' (15 iterations) |
 |
 |
Blobs
| 'F' $\to$ 'FFF-' (15 iterations) |
'F' $\to$ 'FF+F' (15 iterations) |
 |
 |
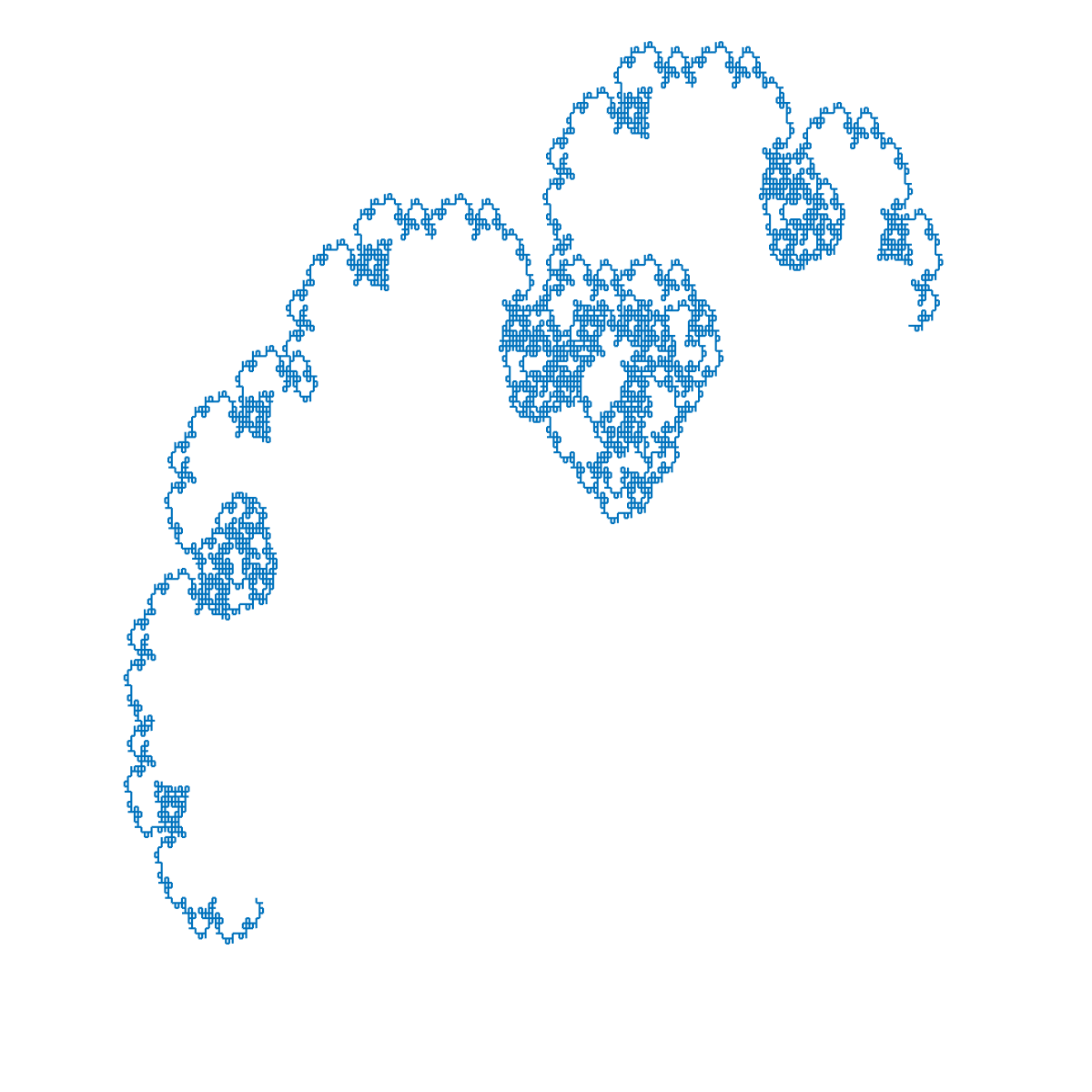
The Levy C Curve
| 'F' $\to$ 'FF+' (15 iterations) |
'F' $\to$ 'F+F-' (15 iterations) |
 |
 |
Fractal-Like Curves
| 'F' $\to$ 'F-F+F' (15 iterations) |
'F' $\to$ 'F+FF-' (15 iterations) |
 |
 |
Some More Complicated Curves
Here are some highlights when we use the larger alphabet {‘F’, ‘X’, ‘Y’, ‘-‘, ‘+’}, instructions as in the dragon curve example, and a rulebook of the form ‘X’$\to$’WORD1’, ‘Y’$\to$’WORD2’.
Fractal-Like Curves
| 'X' $\to$ 'FXY', 'Y' $\to$ 'YX+' (20 iterations) |
'X' $\to$ 'XFY', 'Y' $\to$ 'X-Y' (20 iterations) |
 |
 |
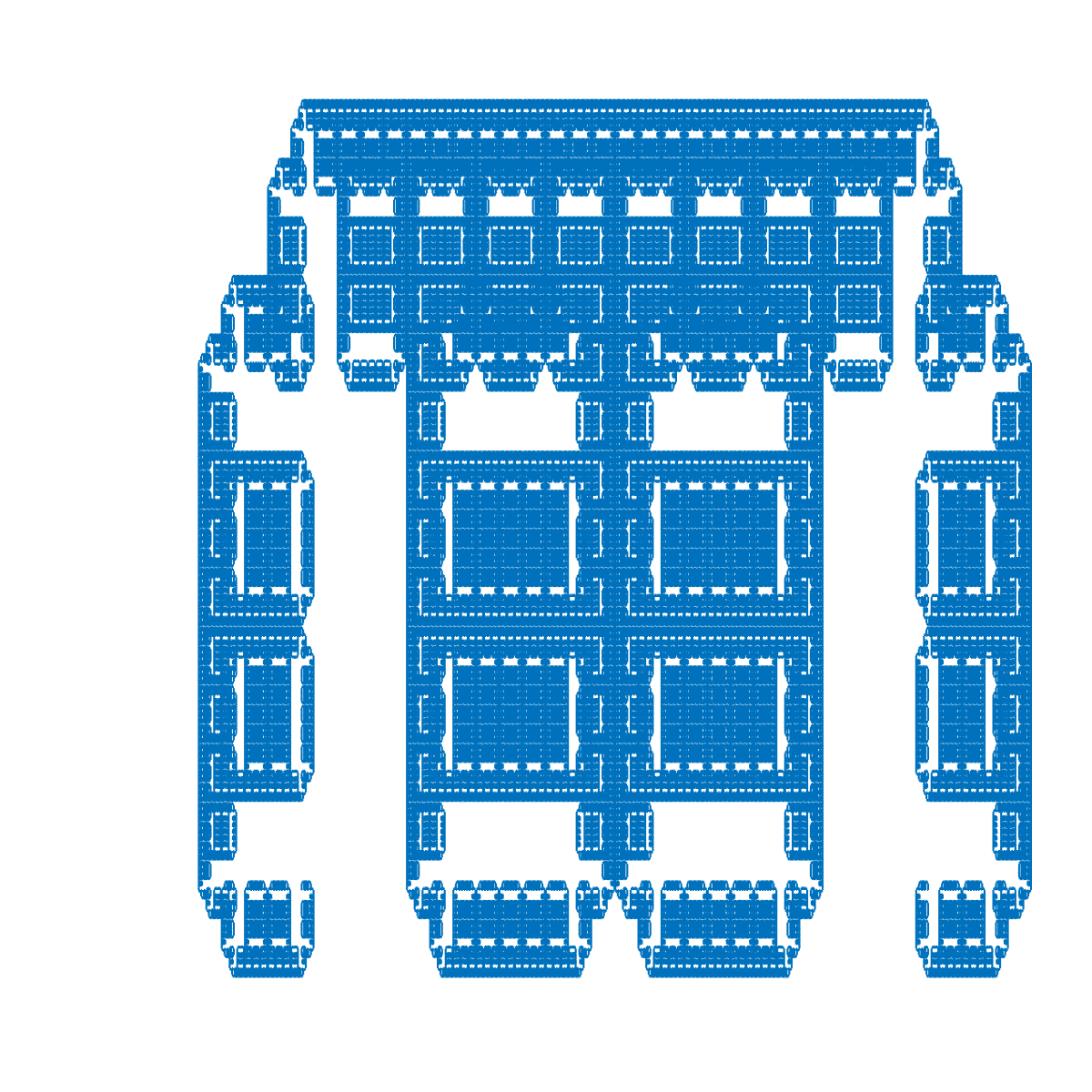
| 'X' $\to$ 'FY+', 'Y' $\to$ 'YXX' (15 iterations) |
'X' $\to$ 'FY+', 'Y' $\to$ 'YXX' (20 iterations) |
 |
 |
| 'X' $\to$ 'FYX', 'Y' $\to$ 'XY-' (20 iterations) |
'X' $\to$ 'YFY', 'Y' $\to$ 'Y-X' (20 iterations) |
 |
 |
| 'X' $\to$ 'FYXY', 'Y' $\to$ 'XY-' (15 iterations) |
'X' $\to$ 'FY', 'Y' $\to$ 'XY-' (20 iterations) |
 |
 |
| 'X' $\to$ 'FY+', 'Y' $\to$ 'XY-' (15 iterations) |
'X' $\to$ 'FY+', 'Y' $\to$ 'XY-' (25 iterations) |
 |
 |
Sierpinski-esque Blocks
| 'X' $\to$ 'FYY', 'Y' $\to$ 'X-X' (15 iterations) |
'X' $\to$ 'FYY', 'Y' $\to$ 'X-X' (20 iterations) |
 |
 |
| 'X' $\to$ 'FY-', 'Y' $\to$ 'XXY' (20 iterations) |
'X' $\to$ 'FY+', 'Y' $\to$ 'XXX' (20 iterations) |
 |
 |
"Chromosomes"
| 'X' $\to$ 'YF', 'Y' $\to$ 'YX-' (20 iterations) |
'X' $\to$ 'YF', 'Y' $\to$ 'YX-' (30 iterations) |
 |
 |
| 'X' $\to$ 'YF-', 'Y' $\to$ 'YX-' (20 iterations) |
'X' $\to$ 'YF-', 'Y' $\to$ 'YX-' (30 iterations) |
 |
 |
| 'X' $\to$ 'FY+', 'Y' $\to$ 'YYX' (15 iterations) |
'X' $\to$ 'FY+', 'Y' $\to$ 'YYX' (20 iterations) |
 |
 |
| 'X' $\to$ 'Y-', 'Y' $\to$ 'YXF' (20 iterations) |
'X' $\to$ 'YF-', 'Y' $\to$ 'Y-X' (20 iterations) |
 |
 |
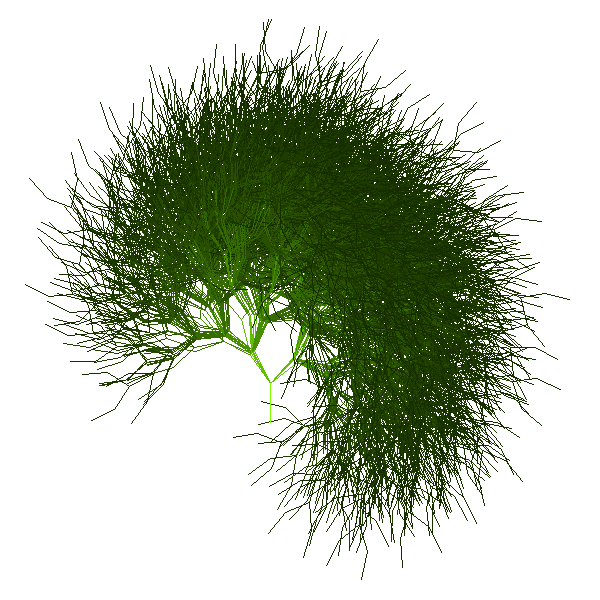
Plants
These turtle curves are somewhat more complicated. Now we have incorporated varying line length and color, as well as “branches” defined by putting words in brackets. The results are plant-like.
More Plants