Surfaces of Revolution

On a surface of revolution given by coordinates $(f(v)\sin(u), f(v)\cos(u),g(v))$ with $v\in\mathbb{R}, u\in[0,2\pi)$, the geodesic equation can be solved by an integral formula. If the geodesic curve $\gamma$ is given by $\gamma(t)=(u(t),v(t))$ in $(u,v)$-coordinates, then it can be shown that either both $v(t)=v_0$ is constant and $f’(v_0)=0$ (such a curve is called a parallel), or

$$u(t) = c \int_{v(0)}^{v(t)} \frac{1}{f(v)}\sqrt{\frac{f'(v)^2+g'(v)^2}{f(v)^2-c^2}}dv + u(0)$$

for a certain constant $c\geq0$. This constant controls Clairaut’s relation: if the velocity vector of $\gamma(t)$ is at angle $\theta(t)$ with the curve $s\mapsto (s, v(t))$ (i.e., the closed curve of constant $v$), then there is some $c$ so that $f(v(t))\cos\theta(t)=c$ for all $t$. A proof of this can be found in M. do Carmo’s Differential Geometry of Curves and Surfaces (Prentice-Hall, 1976). As a special case of the above, if $c=0$ then $u(t)$ is constant, in which case we call $\gamma$ a meridian geodesic.

Below we show some example solutions. The code for these images can be found here, where we solve the integral numerically. In this program, the geodesic is specified by setting $v(0)$ and $c$ and assuming $u(0)=0$. However, when $\cos\theta(t)=1$, then $f(v(t))=c$ and the integrand above is undefined. This corresponds to the case that $\theta(t)=0$ and $v’(t)=0$, and hence that $\gamma$ is potentially turning around (i.e., going from increasing $v$ to decreasing $v$). Therefore a bit of care is needed when evaluating the above integral numerically, since the same interval of $v$ values may be traversed by $\gamma$ multiple times.

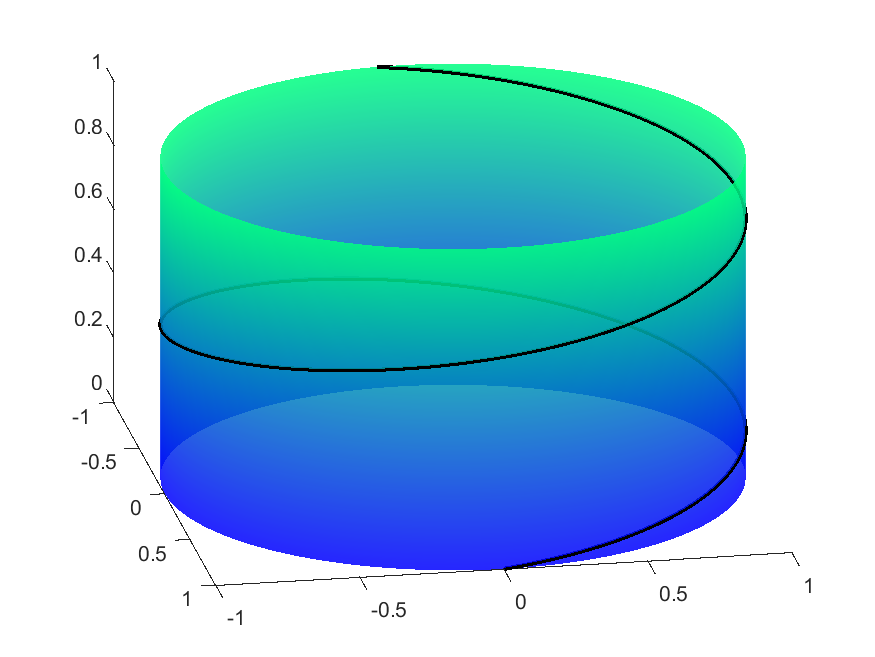
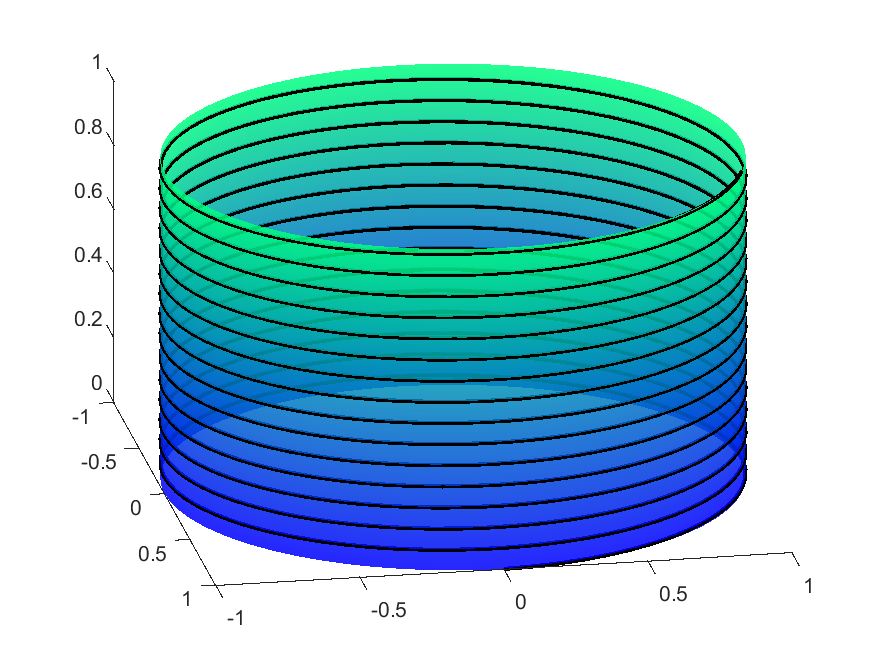
Cylinder

The cylinder is a very simple surface of revolution and the integral above has a closed form:

$$u(t) = \frac{c}{\sqrt{1-c^2}}(v(t)-v(0)) + u(0)$$

Thus the non-parallel, non-meridian geodesics are just helices (spirals), with the angle $u$ increasing linearly with the height $v$.

$f(v)=1,\ g(v) = v$ (Cylinder)

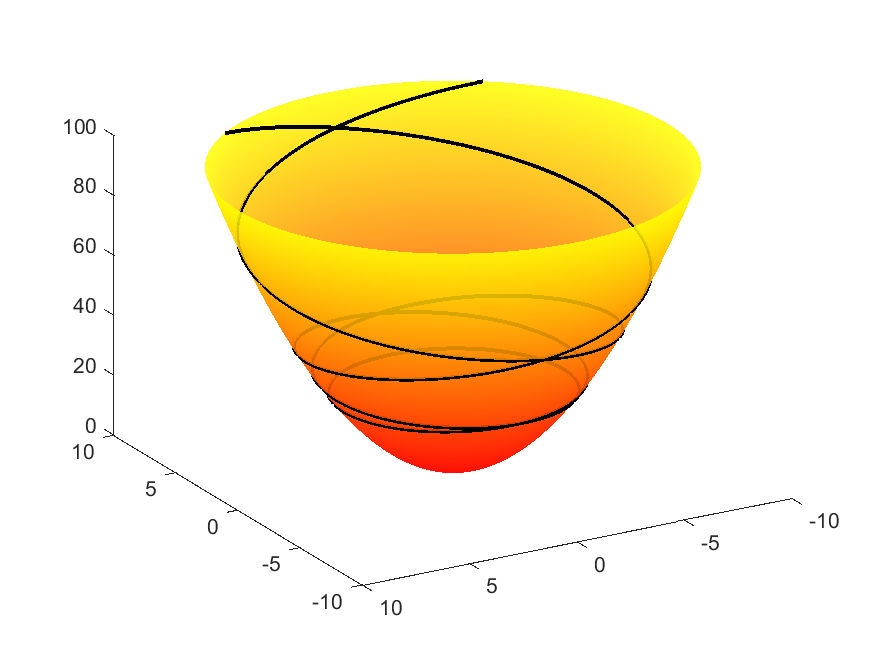
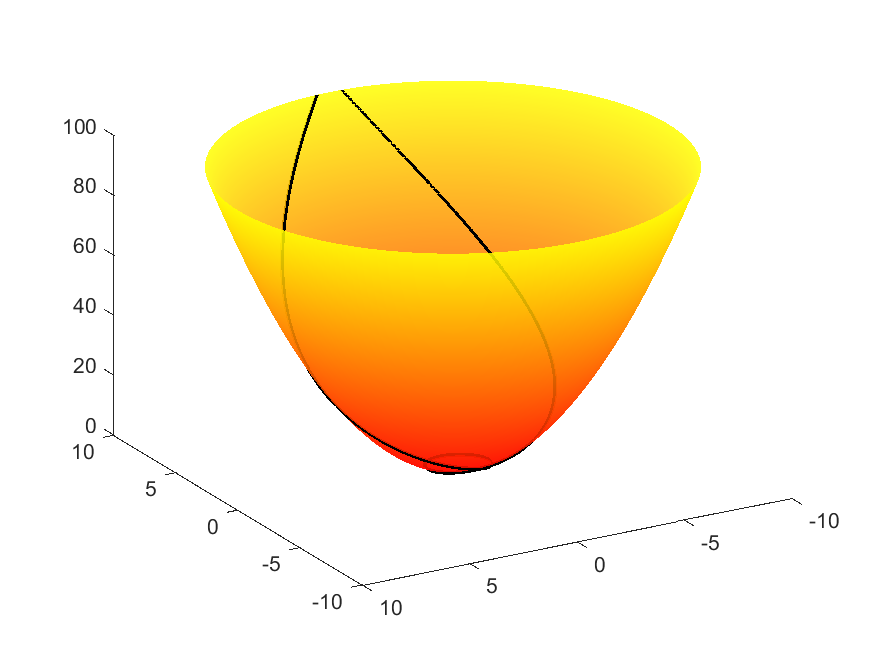
Paraboloid

The paraboloid presents many examples of self-intersecting geodesics. In fact, it can be shown that every non-meridian geodesic self-intersects infinitely many times (cf. M. do Carmo’s Differential Geometry of Curves and Surfaces (Prentice-Hall, 1976)). Since $f(v)$ takes every possible (non-negative) $c$ value at some point, every geodesic is tangent to some parallel. Note that because $f’(v)\not=0$, no parallel is a geodesic.

$f(v)=v,\ g(v) = v^2$ (Paraboloid)

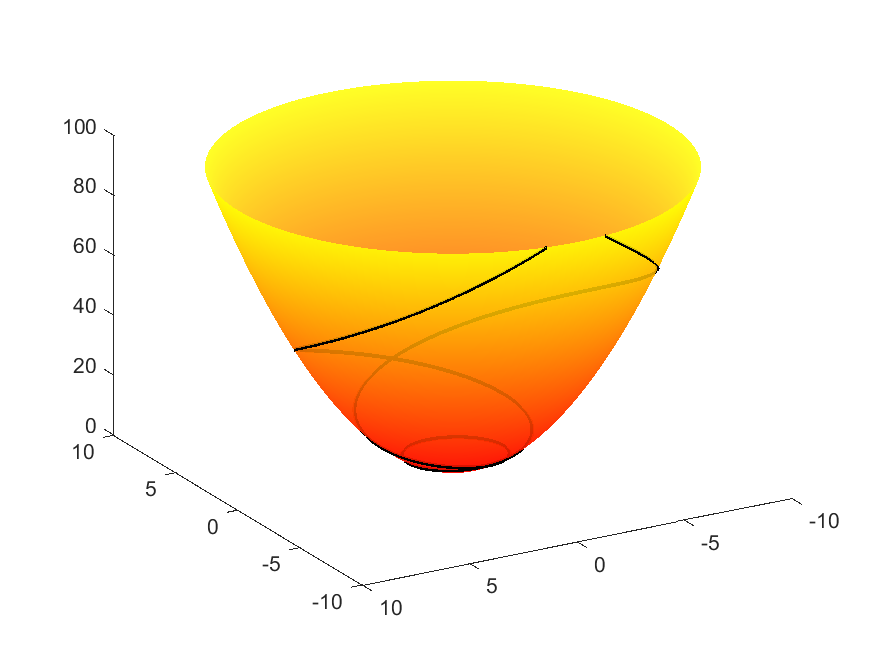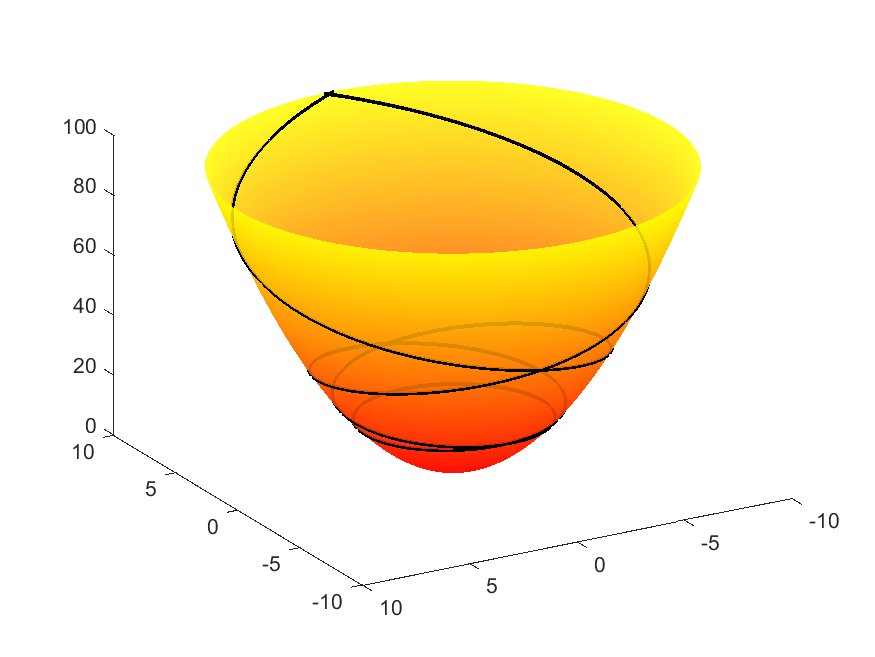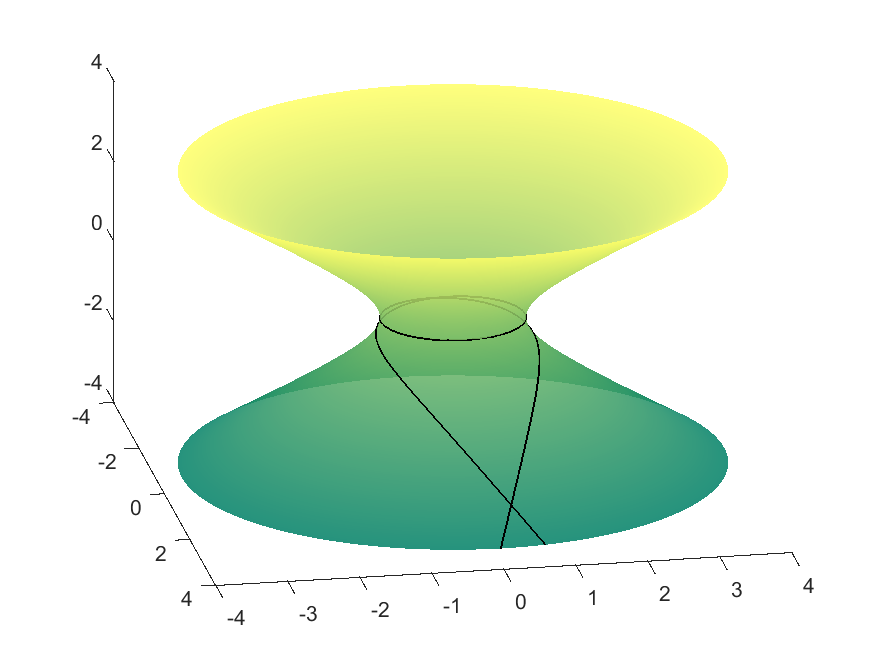
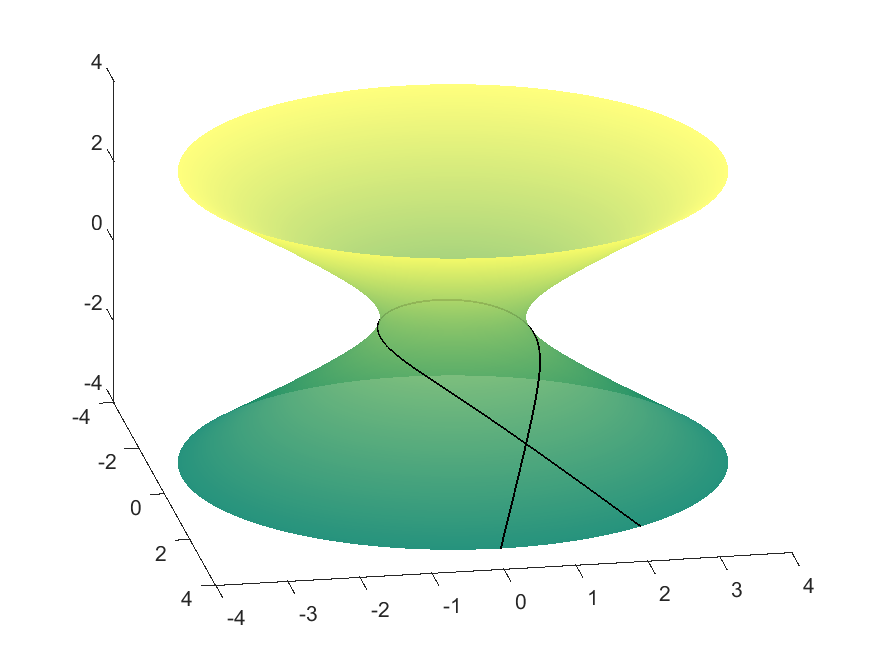
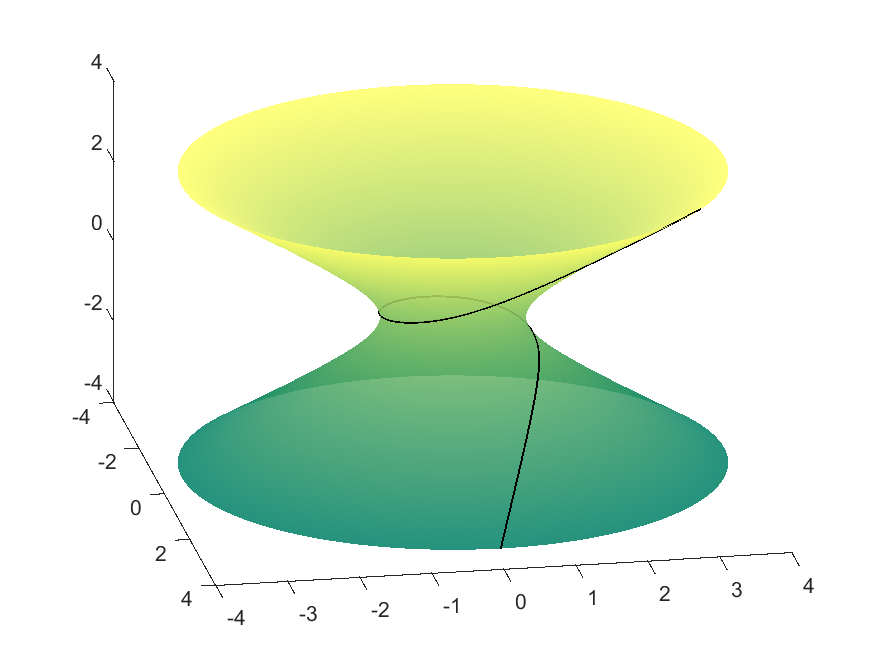
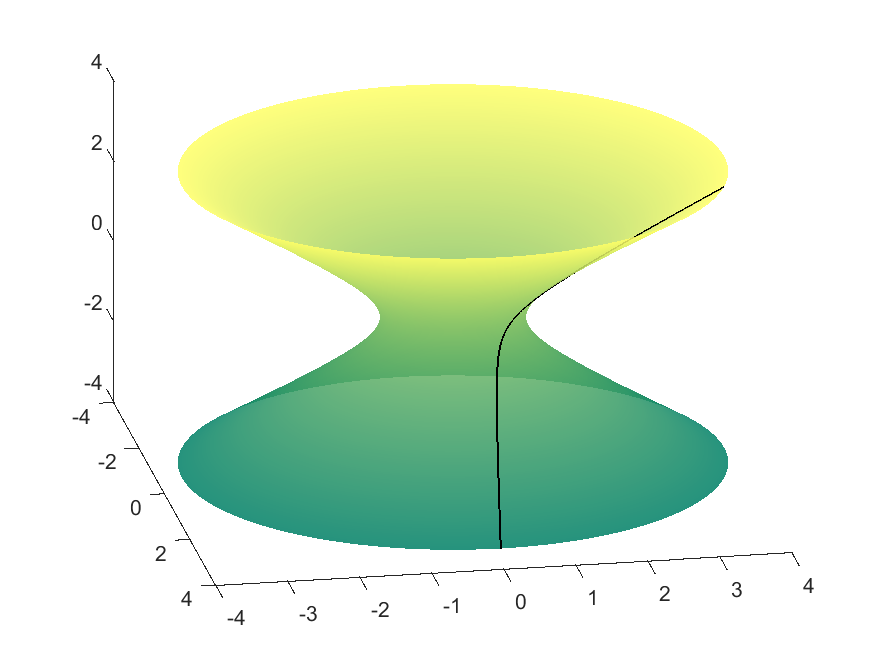
Hyperboloid

In this case, $f(v)\geq 1$. Therefore the geodesics exhibit different behaviour depending on whether $c\in[0,1), c=1,$ or $c>1$. If $c\in[0,1)$, then the geodesic will never turn around and will traverse all $v$ values in $\mathbb{R}$, since $f(v)\not=c$. If $c>1$, then at some point the curve will encounter the $f(v)=c$ parallel and change direction. However, the case when $c=1$ is a bit trickier because the $f(v)=1$ parallel, given by $v=0$, is itself a geodesic since $f’(0)=0$. Because two distinct geodesics cannot be mutually tangent, the geodesic given by the integral equation must never actually reach this parallel. Thus this value corresponds to two geodesics: one approaching $v=0$ from above, and one approaching it from below.

$c=0.9995$	$v=0$ Parallel	$c=1.0001$

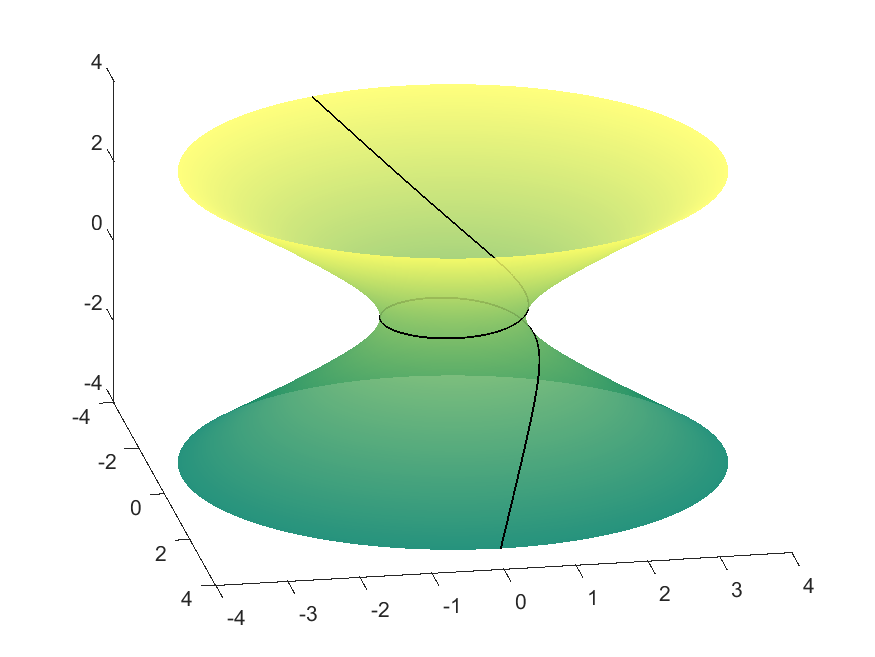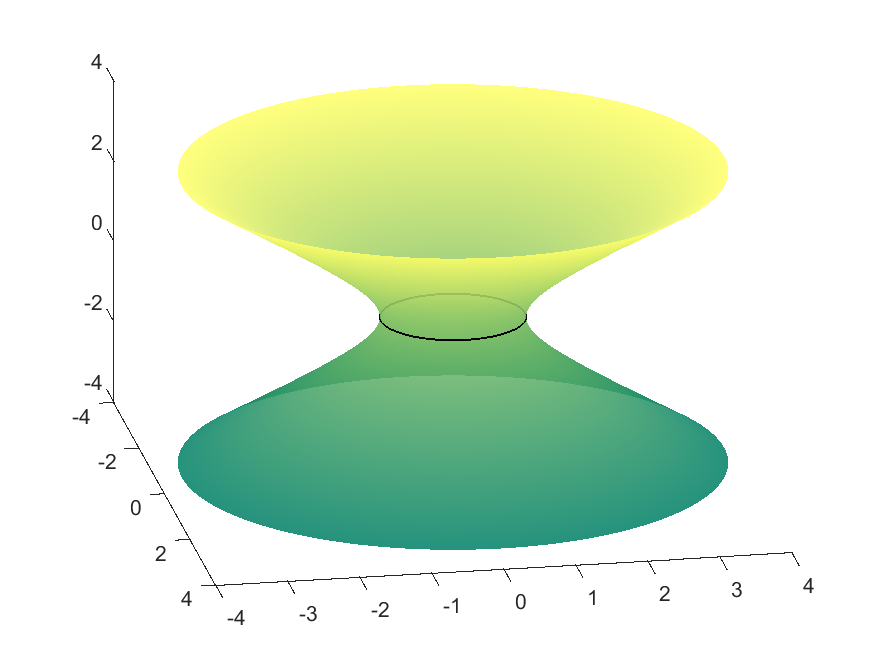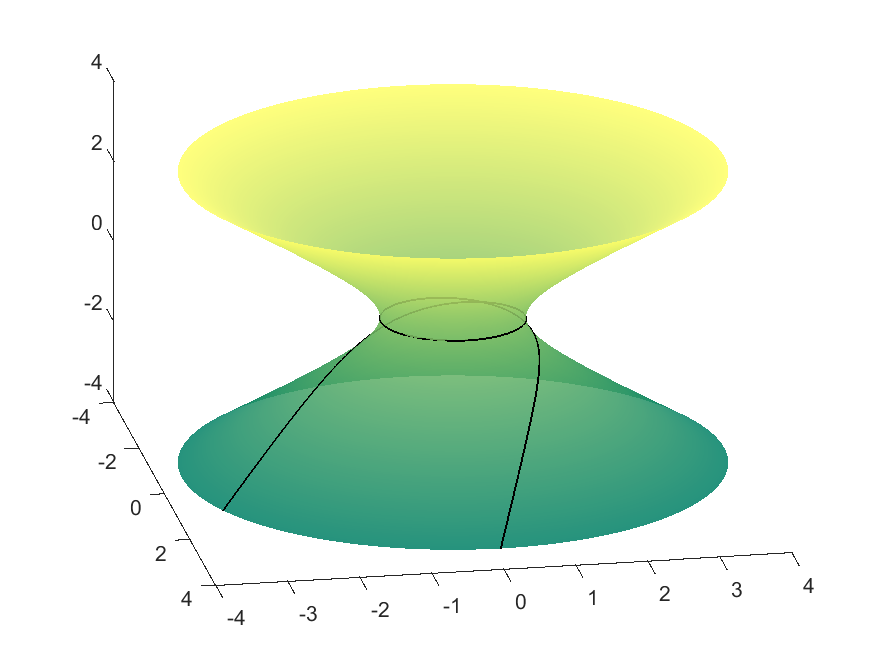$f(v)=\cosh(v),\ g(v) = \sinh(v)$ (Hyperboloid)