Fractals

This page exhibits some Julia and Mandelbrot set fractals. On a mechanical level, the Julia sets are produced by iterating a function $z \mapsto f(z,c)$ at each point, where the initial $z$ value is the given point and $c$ is some global constant. For instance, at each point $z_0$ we could iterate $z \to z^2+1$, obtaining the sequence $(z_0^2+1,(z_0^2+1)^2+1,\ldots)$. Conversely, the Mandelbrot set images are produced by iterating a function $z \mapsto f(z,c)$ at each point, where now the initial $z_0$ is always zero and the value of $c$ changes at each point. The analogous example is $z \mapsto z^2+z_0$, forming the sequence $(0,z_0,(z_0)^2+z_0,\ldots)$ for each $z_0$. For both images, each point is coloured according to how fast the iterations escape to infinity. The code for these images can be found here.

Quadratic Julia Sets

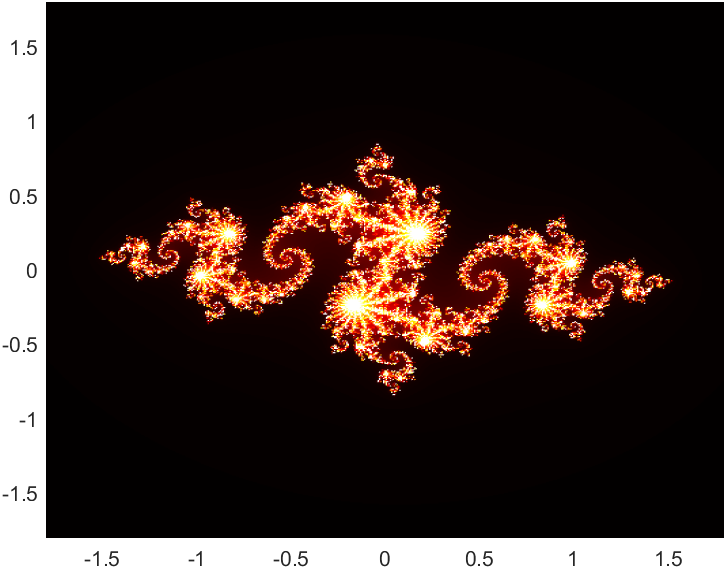
These Julia sets are produced by iterating functions of the form $z \mapsto z^2+c$.

$z\mapsto z^2-0.8+0.156i$	$z\mapsto z^2+0.285+0.01i$

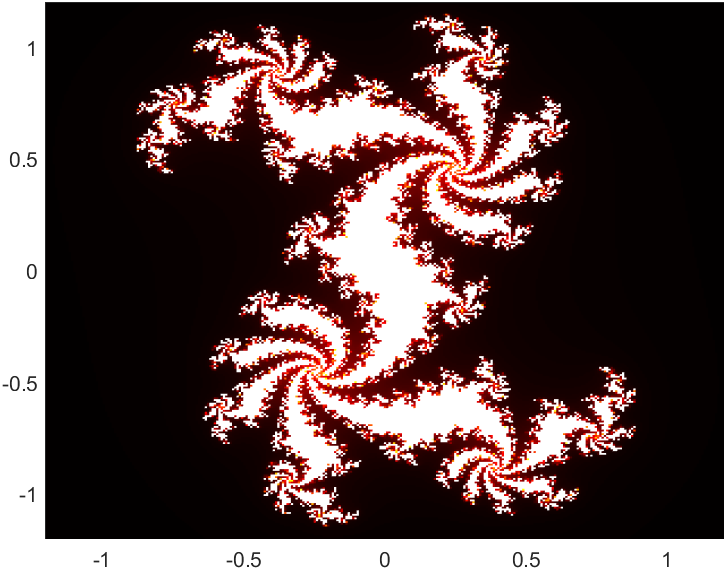
A closer look at a few choice values:

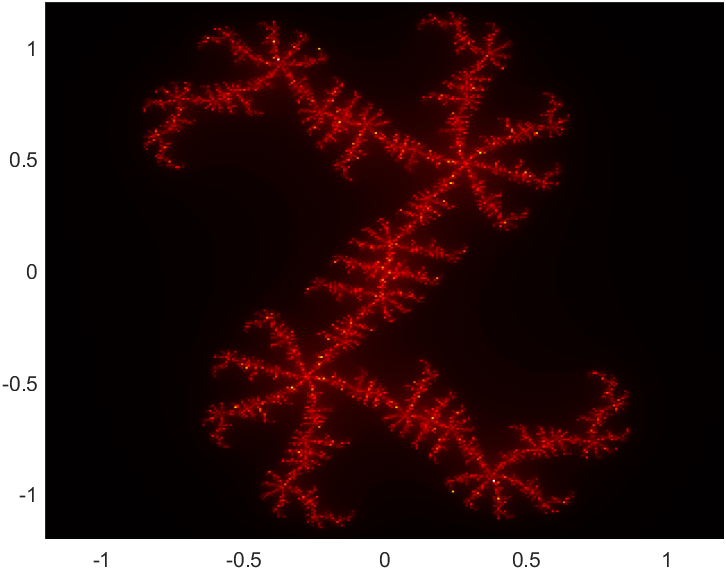
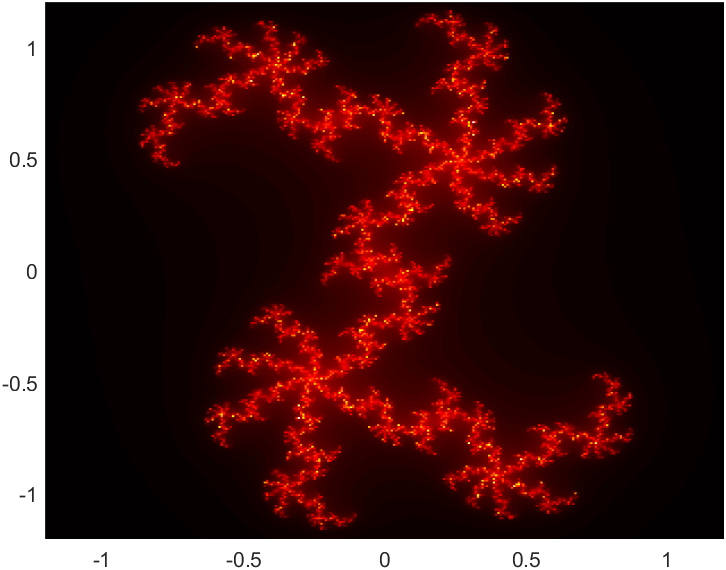
$z \mapsto z^2 + (x+iy)$
	$y=0.19$	$y=0.21$	$y=0.23$
$x=0.39$
$x=0.41$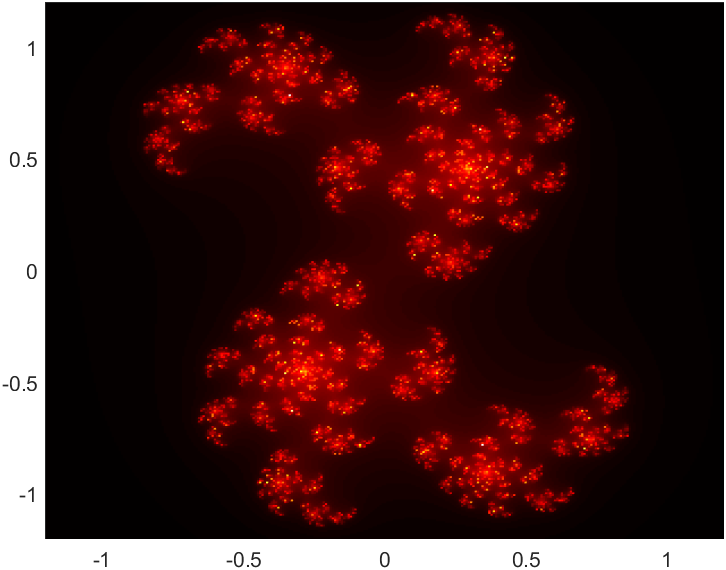
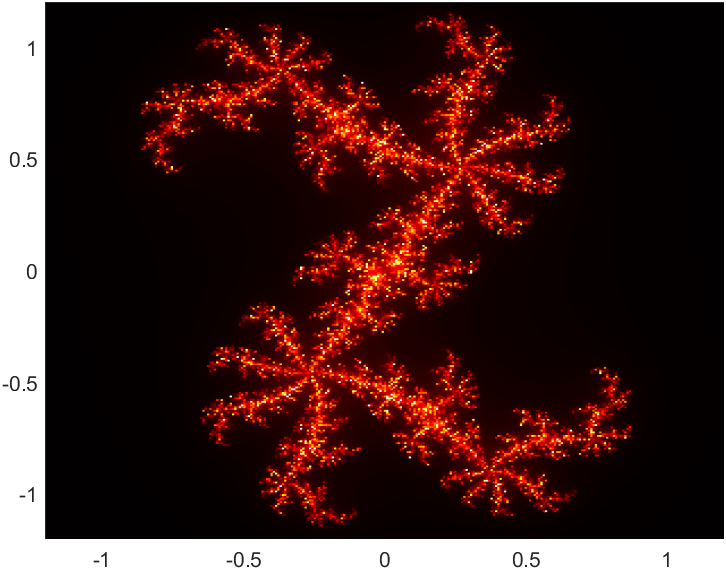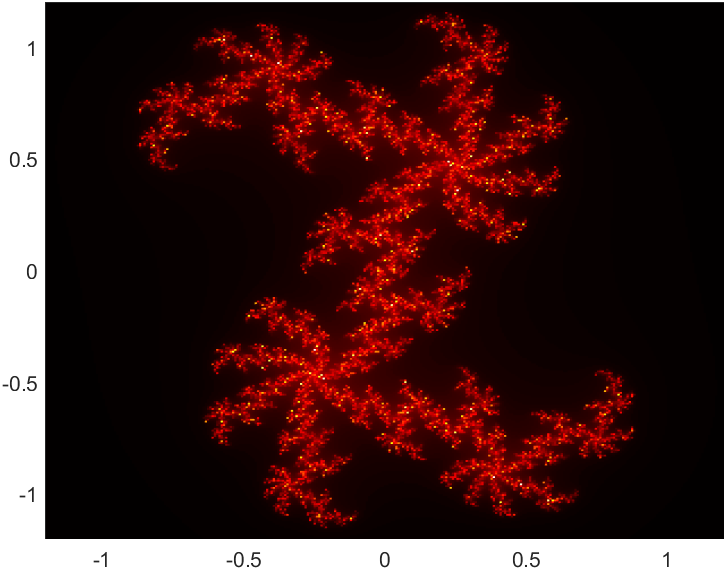$x=0.43$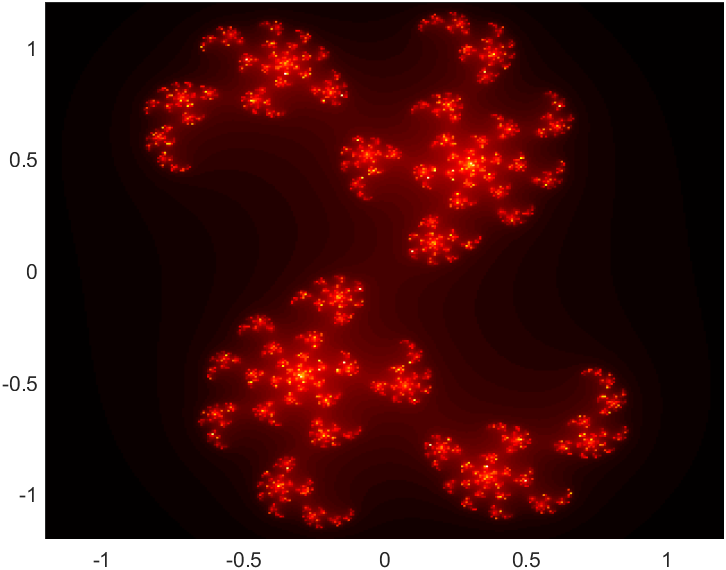

Quadratic Mandelbrot Set

Here we have the Mandelbrot set of the quadratic function $z \mapsto z^2 + c$ instead.

$z \mapsto z^2 + c$

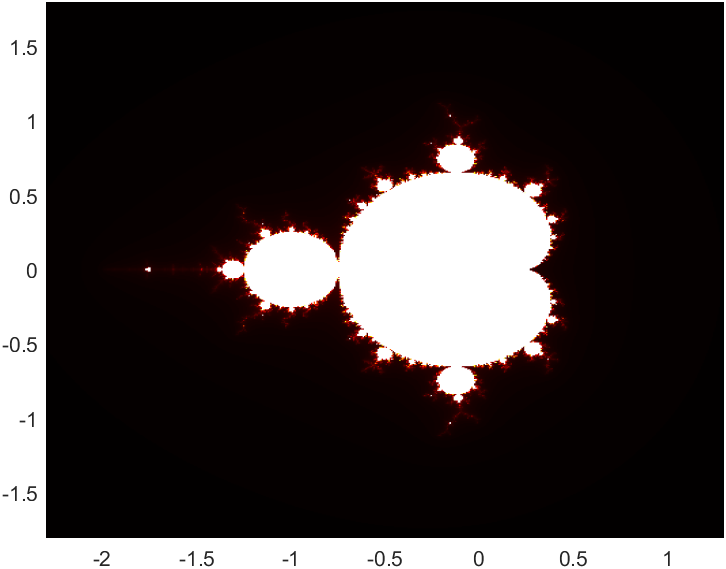Unsurprisingly, the Mandelbrot and Julia sets are closely related. Watch the corresponding Julia set change as we take a diagonal slice through the Mandelbrot set below, following the red dot.

A Diagonal Slice of the Mandelbrot Set

Cosh and Sinh Julia Sets

Other functions, like $\cosh(z)$ and $\sinh(z)$ , also make beautiful Julia sets.

$z \mapsto\cosh(z)-0.9i$	$z \mapsto\cosh(z)+0.4+0.6i$

The $z \mapsto\cosh(z)-c$ Julia Set for $c$ Varying in Time

The Burning Ship

Here is the so-called Burning Ship, which is the Mandelbrot set corresponding to $z \mapsto (|Re(z)|+i|Im(z)|)^2+c$.

The Burning Ship	Zoomed in at (-1.762,-0.028)

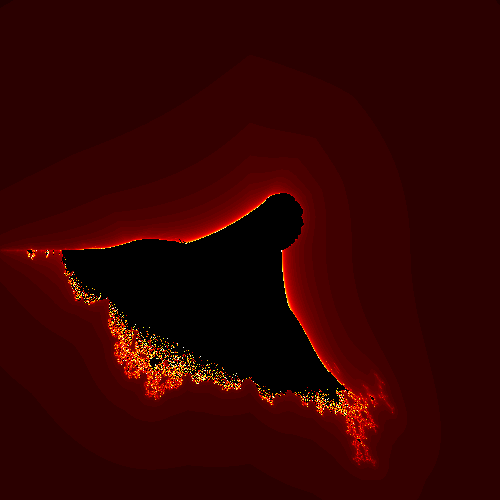Newton's Method

Newton’s method provides a way of finding the zeros of a function $f$– by iterating $z \mapsto z - f’(z)/f(z)$, $z$ will approach a zero of $f$. If $f$ has several zeros, the location of the initial point determines which zero it will converge to. In the following images, each point is coloured with hue corresponding to the zero it converges to and with value (darkness/lightness) corresponding to the speed of convergence.

$z \mapsto z^2-1$	$z \mapsto z^3-1$
$z \mapsto z^4-1$	$z \mapsto z^5-1$

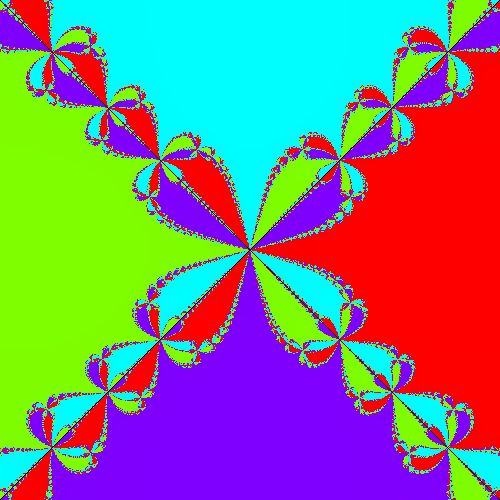Here are some animations of the effect of perturbing $z \mapsto z^3-1$, where $k$ varies in time from -1 to 1.

$z \mapsto z^3+k$	$z \mapsto z^3+kx-1$
$z \mapsto z^3+kx^2-1$	$z \mapsto kz^3-1$

You can also do non-polynomial functions, and control the darkness of a pixel by the speed of convergence of the associated point (in this case, taken mod 2 to produce dark bands).

$z \mapsto \cosh(z)-1$	$z \mapsto \sin(z)$