Hyperbolic Geometry

The orientation-preserving isometries of the hyperbolic plane are the Mobius maps with real coefficients and determinant 1. There are 3 types, and they are characterized by their trace.

Type	Elliptic	Parabolic	Hyperbolic
Trace	|Tr| < 2	|Tr| = 2	|Tr| > 2
Example	$z \mapsto e^{(i\pi/2)}z$	$z \mapsto z+1$	$z \mapsto 2z$
Orbit Diagram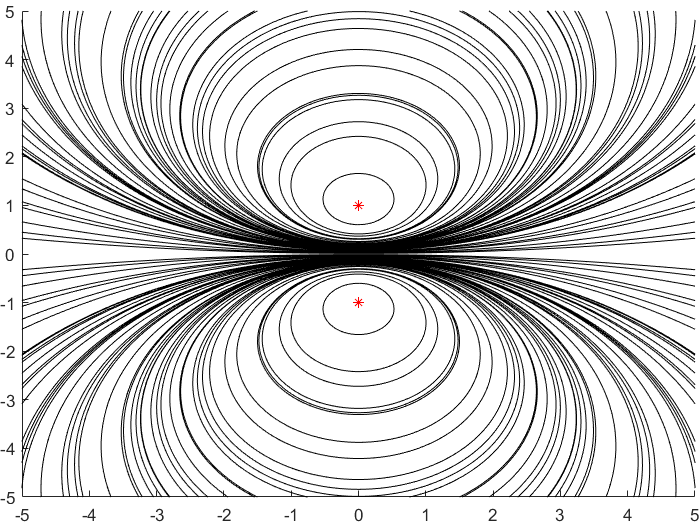

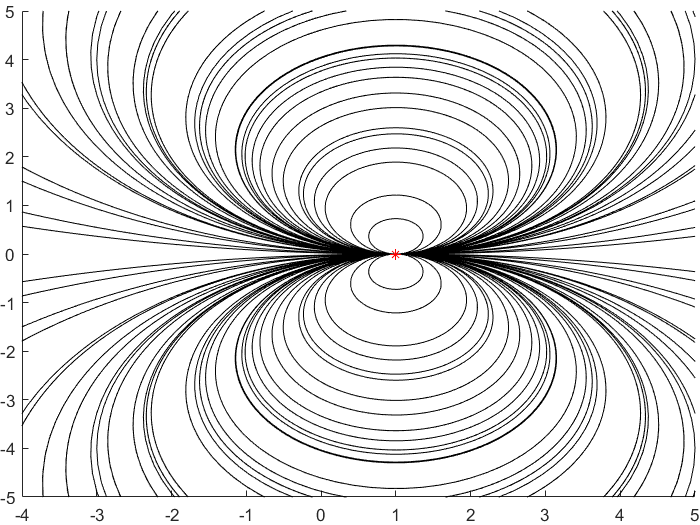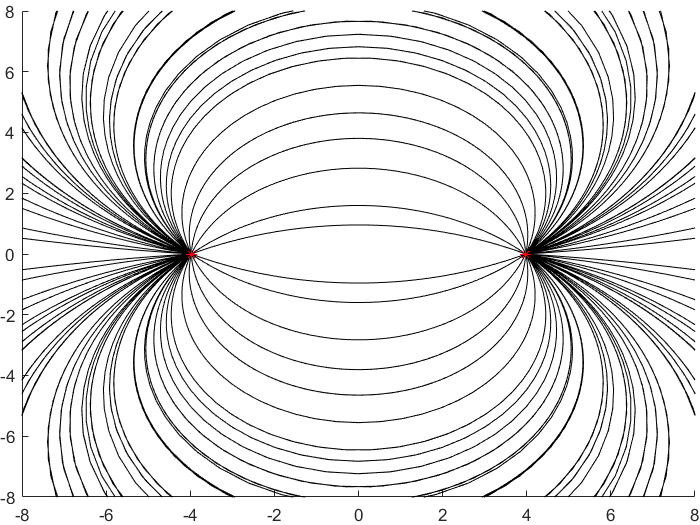Hyperbolic Tilings

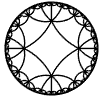
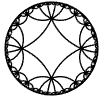
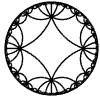
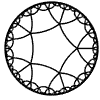
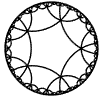
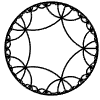
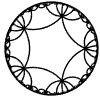
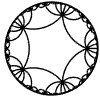
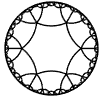
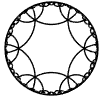
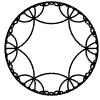
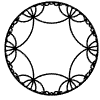
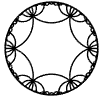
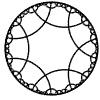
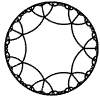
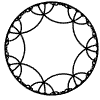
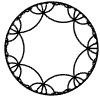
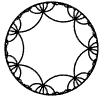
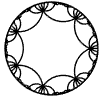
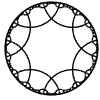
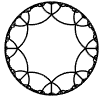
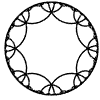
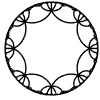
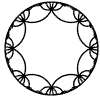
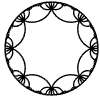
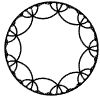
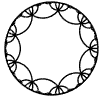
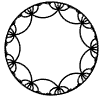
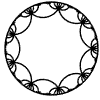
Just as the Euclidean plane can be tiled by (certain kinds of) regular polygons, so too can the hyperbolic plane. Moreover, the action of Fuchsian groups on hyperbolic space can induce tilings of the hyperbolic plane by their fundamental domain. Regular tilings on any surface can be characterized by their Schlafli symbol $(p,q)$, where $p$ is the number of edges of each polygon and $q$ is the number of polygons meeting at each vertex. Only some symbols admit tilings for a given surface, however. The below are some regular tilings of the Poincare Disk model of hyperbolic space. The code for these images can be found here.

p\q	3	4	5	6	7	8	9	inf
3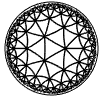
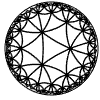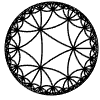4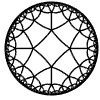
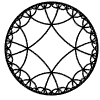5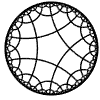
6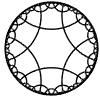
7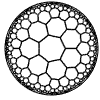
8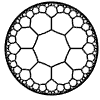
9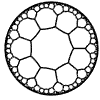

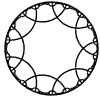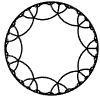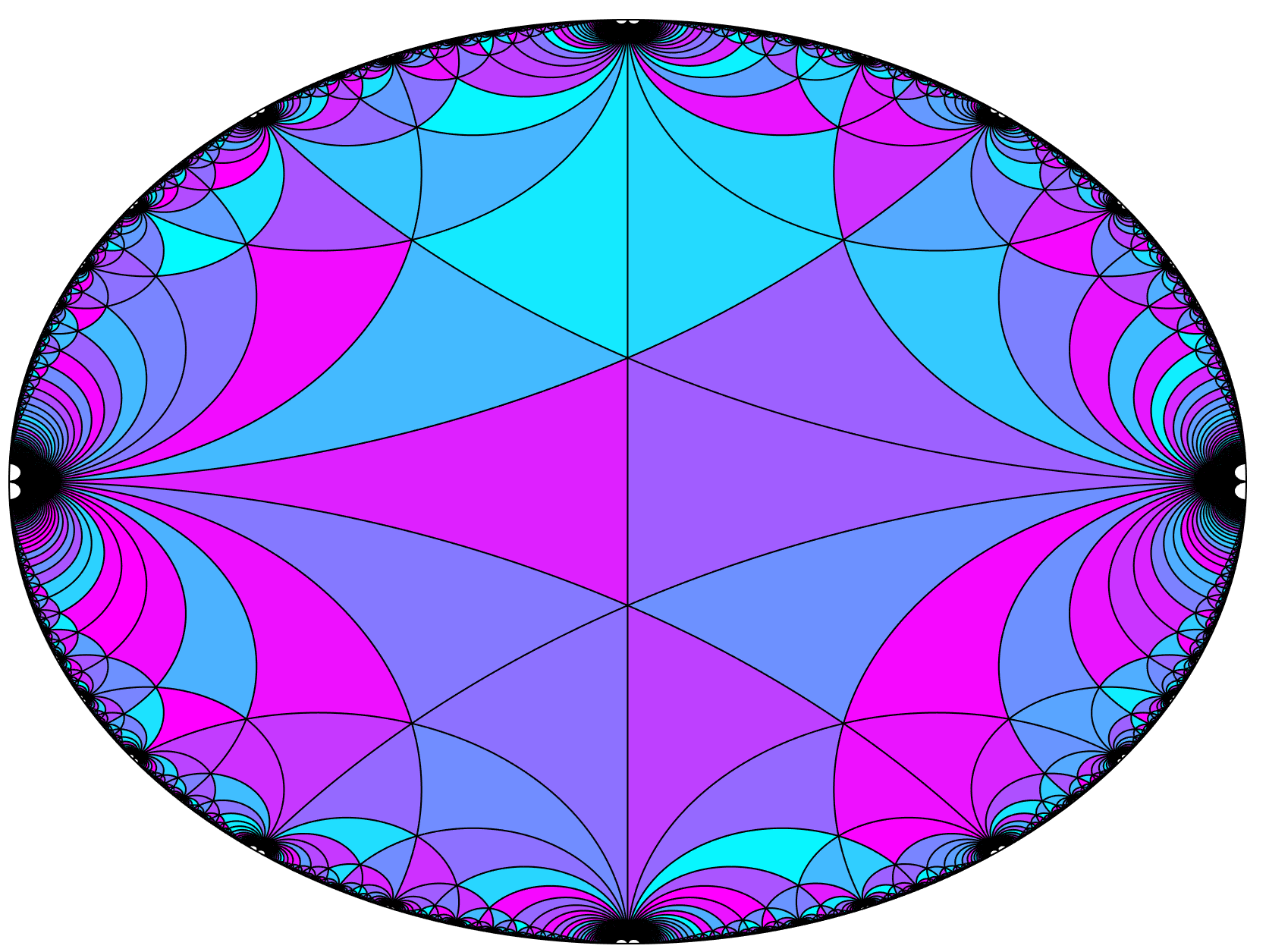
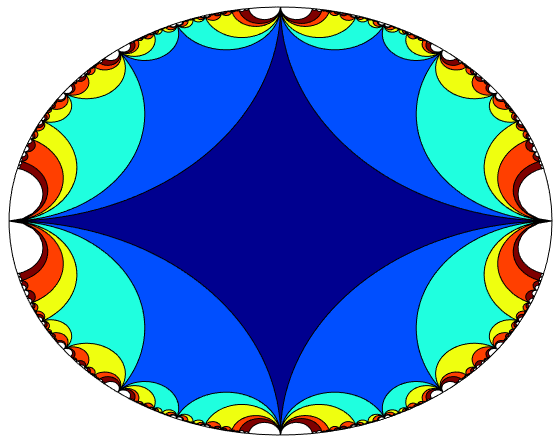
Fuchsian groups of isometries also induce tilings, where each tile is a copy of the group’s fundamental domain. The placement of the tiles is determined by the action of the group: each tile corresponds to the image of the original fundamental domain under a single group element.

The Action of $SL(2, \mathbb{Z})$	The Action of a Punctured Torus Group